On the Johnson Motor and Systems Far from Equilibrium With their Active Environment

On the Johnson Motor and Systems Far from Equilibrium With their Active Environment 

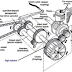
Johnson did produce a permanent magnet rotary motor that turned itself, without holding the magnet. I clamped the magnet on my kitchen table, and the device rotated for over an hour. Since its bearings were very crude (old lazy Susan for a turntable), that was sufficient. He showed this device to only three persons. There was a break-in at his lab, and guess what was taken: the only working model he had.

His real problem over the years has been hand-cutting of magnets and magnet assemblies. The effect he is using has to have very great precision to obtain, and then one has to do it multiple times, because the variation in the magnets themselves is more than an order of magnitude greater than the precision required.

And he is not using simple magnetic repulsion and attraction; for that effect, everyone knows that a closed circle yields a closed line integral of the force which integrates to zero; in short, a conservative field. Johnson seeks to evoke the exchange force by sudden spin flipping, which momentarily (when evoked) fires and has a thousand times or more strength (for a moment) than the magnetic field. Even macroscopically, this force in close tolerances can reach up to 100 times the magnetic field force, momentarily. Check out the exchange force, e.g., in Feynman's three volumes of physics.

Johnson is a very fine person, very religious, and he has also been fairly ill. He's getting well along in years, and I do hope he will get the precision machining he requires, to complete his project before he passes on.

His reason for using different kinds of magnets cut into pieces and making assemblies is that in some of these he is able to evoke the exchange force very sharply, in the direction desired (controlled by the exact assembly of different magnetic materials interacting with each other). He has also had his project effectively sabotaged on more occasions than one.

For those interested in Johnson's approach, be aware that you must first have a schema that will or can produce a nonconservative magnetic field, when the force as a line integral is integrated around the entire closed path to a real nonzero value. Otherwise, if one is just thinking poles and repulsion and attraction, forget it.

There are over 200 effects in magnetic materials; it is not a simple subject at all. About half of those effects are well-understood. Some of the others are fairly well understood, some a little understood, and some not understood at all.

Also, multivalued potentials arise naturally in the magnetic theory itself. If a multivalued potential can occur in a rotary system so that it affects the line integral, then one has an integration to a non-zero and self-rotation is indicated. Eerily, magnetics scientists and theorists think this capability is a great nuisance, and they "twist" the magnetic theory itself in all sorts of ways to try to eliminate those multi-valued potentials.

Nonetheless, when not arbitrarily manipulated, the theory does predict and permit permanent magnet motors that self-rotate. There is no problem with the source of the excess energy; any dipole (including a permanent magnet dipole) has a scalar potential between its ends, and the Whittaker decomposition in 1903 of that potential shows very clearly that it is a set of bidirectional longitudinal EM phase conjugate wavepairs. 

But let's look a little further at a "phase conjugate wavepair" than Whittaker did or his modern interpreters have done.

The phase conjugate actually exists in the imaginary plane, prior to its observation. After observation (interaction with charged matter—in this case, interaction with magnetic charge which one may just think of as "pole"), one has shifted the wave from the imaginary plane (in 4-space, from the time-domain) into real 3-space, and inverted its direction. We thus observe it as an outgoing real EM wave, as Whittaker noted, and since it is observed as antiphased in 3-space from its twin in the wavepair, that leads to the ubiquitous but erroneous interpretation of that decomposition as being bidirectional EM wavepairs in 3-space.

Actually, this is just one example of an enormous error in modern physics: the substitution of the effect (the observed wave, after interaction with an observable—e.g., charged mass—has occurred) for the cause (the wave-as-it-exists-in-spacetime, before the interaction and coming in to the charged mass to interact with it). If we correct that ubiquitous error of misinterpreting the causal wave, which is actually incoming prior to parity reversal by the observation process, the "input" or causal wave before interaction turns out to be that incoming phase conjugate wave in the complex plane. It is incoming if we do not go ahead and shift it into 3-space, by assuming that the interaction with the magnetic charge has occurred and observation has been accomplished.

So the rigorous interpretation of the Whittaker 1903 decomposition is that the potential between the poles of a magnetic dipole is comprised of a harmonic set of incoming longitudinal EM waves in the time domain. We can easily experimentally prove that no waves are coming into the magnet from 3-space, because none can be detected by our instruments. It is also a fact (if we do not push the analogy too far) that the charge spins 720 degrees. It spins 360 degrees in the complex domain (i.e., the time domain) and then flips into 3-space and spins another 360 degrees [The spin is not a "flat" spin like a disk, but rather like a 3-d circulation]. At any rate, the charge absorbs the incoming Whittaker phase conjugate half-set energy while spinning in the time (complex) domain, and then re-emits its excitation energy in 3-space when it rotates there.

This is the solution, by the way, to what has been called by Sen and others the most formidable problem in classical and quantum electrodynamics: the problem of the association of the fields and potentials and their energy, with the source charge (or the source dipole). I solved that problem and published it. Normal electrodynamics, by failing to make the correction to the misinterpretation of the phase conjugate wave, but placing it in 3-space (where it is assumed that the wave has been observed and is an effect a priori), could not resolve it. The conventional interpretation just assumed two effect waves, instead of a cause and effect pair of waves. In that case, the continuous emission of EM energy by a source charge or dipole, in all directions in 3-space, has no possible solution because it has become a gross violation of the conservation of energy law. 

So instead of solving the problem, all our present electrodynamics texts (including graduate level) implicitly assume that the source charge (or source dipole) just sits there and creates all that energy it continuously pours out to form its fields and potentials.

Either we solve the problem of the source charge and source dipole, or else we must completely abandon the conservation of energy law. We have indicated how to resolve the issue and save the conservation of energy law.

One can easily show that a permanent magnet or any other dipole does continuously pour out energy. Do a gedanken experiment. Take a radial line away from an origin point in the lab, and set instruments at, say, every light second distance, out to a light year away. Now suddenly form that dipole (or source charge) at the origin. One second later, the first instrument reads the presence (arrival) of a field. But it stays at that level from then on. Two seconds after dipole formation, the second instrument reads, and stays at that level from then on. Etc. Wait one year, and a volume of space a light year in radius has been filled with EM energy, and that energy is still ongoing.

Any charge also is just a set of continually occurring dipoles, when the virtual charges of opposite sign that are clustered around it in the vacuum are considered. Take one of those virtual charges while it exists, and take a differential piece of the observable "isolated" charge at the center of the clustering. Those two form a dipole, and the same remarks as above apply. So the "isolated charge" is just a set of such composite dipoles, each with one end momentary and the other end continuing through coupling with many successive virtual charges. Each composite dipole while it exists has a scalar potential between its ends, and that scalar potential involves our reinterpretation of Whittaker's 1903 decomposition of it.

Any charge or dipole thus continuously receives enormous unusable energy from the vacuum, and pours it out continuously in all directions as usable EM energy, so long as the charge or dipole remains intact. Original charges and dipoles have been pouring out energy that way for some 15 billion years or so.

A good text will in fact show an indication of the enormous EM energy flowing in space around every circuit or transmission line. Kraus shows numbered contours in the energy flow through the space surrounding a standard transmission line. By definition, if we place a unit point charge at a point in space on one of those contours, the contour number represents the power in watts per square meter that will be intercepted and collected at that single point, by that unit point static charge. If we place a charge of 100 unit point static charges at that same point, we will collect 100 times as much energy on that charge as we did on the unit charge before. These contours presented by Kraus are all on energy flow lines where the energy flow misses the entire circuit, and is just wasted.

For your very best professor, challenge him to try to calculate the total EM energy that can be collected by intercepting/collecting charges in space around a simple little battery-powered circuit consisting of two lines from the battery to a pure resistor. Or try to find it in any paper or text anywhere.

Poynting never even considered the vast energy flow component that misses the circuit entirely and is wasted, but assumed only that small component of the energy flow that actually gets intercepted and enters the circuit.

Heaviside discovered that missing huge component shown by Kraus, but was very cautious. In a simple nominal case, there is about 10 trillion times as much energy flow missing the circuit altogether, but pouring out of the terminals, as actually strikes the surface charges of the conductors and gets diverged into the wires to power the circuit. 

The problem in the 1880s was, where on Earth could such an enormous energy flow possibly be coming from? Remember, scientists had not discovered the atom and electron yet, and "space" was considered to be filled with a thin material fluid. Time was considered to flow immutably, and there was no such concept as "energy flow in the time domain". Nor had Whittaker yet performed his mathematical decomposition of the scalar potential, nor had he yet initiated superpotential theory. Anyone could estimate or calculate how much energy was input to the shaft of a generator, and no one was going to believe that trillions of times as much energy as that input would and did emerge from the terminals of the generator and fill all space around the connected external circuit.

Heaviside, though brilliant, was self-taught and never attended university, so he was very cautious and did not wish to be accused of being a "perpetual motion nut", which would have destroyed him. There were only about three dozen electrodynamicists at the time on the entire planet earth. So Heaviside spoke of the "angle" of the tiny amount of energy flow entering the circuit and powering it, and the "angle" of the enormous energy flow that remained and did not enter the circuit at all. But it is crystal clear that he knew the enormity of the extra energy flow that missed the circuit and was not utilized at all.

There was no such thing in the 1880s as a theory of the active vacuum. Special and general relativity and quantum mechanics were not even conceived yet, much less born.

The greatest electrical scientist of the day was H.A. Lorentz. He understood Heaviside's work, but had exactly the same problem with any reasonable source for the startlingly large nondiverged energy flow around a circuit. In no way could he account for this enormous energy flow emerging from the terminals of a battery or generator. And even the great Lorentz could not afford to just advance this openly, lest he also be labeled a "perpetual motion kook" and scientifically destroyed. So unable to solve the problem, he simply found a way to discard it and avoid it entirely. He reasoned that the "Heaviside" extra component of flow that missed the circuit "had no physical significance" (his words) since it powered nothing at all.

So Lorentz integrated the energy flow vector itself around a closed surface assumed around any little volume element of interest. As can be seen, this zeroes any nondivergent vector, and the "enormous Heaviside extra vector" component is nondivergent since it hits nothing at all. The Poynting vector component, however, is diverged a priori, since Poynting started with that precise assumption. Hence the Poynting vector emerges, and the Heaviside "dark unaccounted energy flow" vector disappears from accountability.

Electrodynamicists still use that Lorentz trick to get rid of that embarrassing wasted energy flow, as do electrical engineers.

As can be seen, Heaviside's and Lorentz's "dark energy flow" problem is essentially the same beast as the missing beast that has been responsible for the "problem of the source charge or dipole and its associated fields and potentials and all that energy in them". Now we have it. And we also have the mechanism for simple, easy extraction of enormous EM energy from the vacuum, at will, anytime, and anywhere in the universe. And cheaply.

We do not have an energy crisis. We have an energy flow accounting, intercepting, and using crisis because our energy scientists are still using an EM energy flow model that has been mutilated for more than a century. Classical electrodynamics does indeed need the kind of vigorous rework that was strongly recommended by Bunge as follows: "...it is not usually acknowledged that electrodynamics, both classical and quantal, are in a sad state."

Further, our solution to the problem of the source charge and the source dipole ties in directly with particle physics, where in the 1950s broken symmetry was discovered (then we did have quantum mechanics and a theory of the active vacuum, fairly well along). In particle physics it is well-known that any dipole is a broken 3-symmetry in its fierce energetic EM exchange with the active vacuum. By the very definition of broken symmetry, this means that some of that "disintegrated" (virtual) energy continuously absorbed from the vacuum by the charge or dipole, is not re-radiated back in disintegrated (virtual) form. Instead, it is integrated (by the spin of the charge) and, when the charge enters 3-space in its spin cycle, re-emitted as observable, real EM energy in all directions.

So our solution to what has been called the biggest problem in electrodynamics is consistent with everything known so far. And it also saves the conservation of energy law.

Note also that in 4-space theory the 4th axis is modeled as -ict, so the i reveals the imaginary plane connection, the c reveals the compaction of the dimension itself, and t is the only variable. Hence any EM energy flow along that axis is a flow in and within t, the only variable.

This directly affects and changes the electrical engineer's interpretation of "reactive power" as being a real wave after observed in 3-space. Yes, that wave does exist after interaction with charges. But prior to that interaction, the real hidden "reactive power" is in fact a wave in the time domain (complex plane, 4th axis). We might thus adopt the term "pre-reactive power", to differentiate it from the present interpretation (after observation, as being an effect rather than a cause) by electrical engineers.

The solution to the charge and dipole problem also is of direct importance to free energy researchers. There is no such thing as COP>1.0 in a system in equilibrium with its active vacuum environment . Classical EM does not even model the vacuum exchange with the system, much less a broken 3-symmetry in that system. Maxwell's original equations and Heaviside's severe curtailment of them, still included two kinds of Maxwellian systems: (1) those in equilibrium with the active vacuum (unknown at the time), and (2) those far from equilibrium with the active vacuum. 

But the Maxwell-Heaviside theory is awkward; variables are unseparated, and closed solution is very difficult and nigh impossible. This means heavy use of numerical methods was required, a terrible thing in those early days without computers. So here again Lorentz stepped in, and "symmetrized" the Maxwell-Heaviside equations by changing them once again. By imposing symmetrical regauging, Lorentz selected only that half-set of the Maxwell-Heaviside theory that represented systems in equilibrium with the active vacuum. The alteration of the potentials just so that the two extra forces appearing were equal and opposite, meant that a "genie" or "demon" had also been assumed—to insure this very presence of just those exact two equal and opposite forces from direct alteration of the potential energy of the system—to enforce that equilibrium with the vacuum. All the rest of the Maxwell-Heaviside systems—specifically, those far from equilibrium with the vacuum—were thus arbitrarily discarded by Lorentz.

Electrodynamicists have continued to use that "symmetrized" subset of the Maxwell-Heaviside theory, because the resulting equations allow the variables to be separated and closed analytical solutions to be obtained. Further, most of the electrodynamicists still are inclined to the view that such "symmetrical regauging" does not change the fundamental theoretical model or what is being modeled. That of course is erroneous.

In short, the electrodynamicists themselves almost universally continue to discard—more than a century later—all those permitted Maxwellian systems that are open systems freely receiving and using energy from the active vacuum.

It can easily be shown that the standard closed current loop circuit rigorously enforces symmetry during the excitation discharge of the excited circuit. The initial excitation (potentialization) is of course a violation of the Lorentz condition. We point out that the vacuum, having an energy density, is just an enormous scalar potential. Any EM potential we make, is a change to that vacuum potential, or a change to an intermediate potential that is such a change. So with potentials, we deal with the active vacuum and its energy, whether we realize it or not. And when we change the local energy density of the vacuum/spacetime, we invoke general relativity and spacetime curvature whether we realize it or not.

The real reason for usually unsuccessful unification of electrodynamics and general relativity is the failure to correct the many flawed assumptions in electrodynamics. General relativity also needs a little extension. For example of a good unified theory and one that is engineerable, one should refer to Sachs' [[i]] unified field theory and particularly to the Evans' [[ii]] union of O(3) electrodynamics with Sachs' theory, as a very important subset of Sachs' theory .

Other interesting things resulting from the solution to the source charge problem are: (1) propagation of EM energy through 3-space is quite different than what we presently assume in physics. Specifically, there is no such thing. Instead, there is the propagation from the time domain to successive differential points or regions in space. More on that sometime in the future. (2) All EM energy appearing anywhere in 3-space, has entered there from the time-domain. (3) EM energy flow and currents in the time domain are more fundamental than EM energy flow and currents in 3-space. A priori, anything in 

3-space is or has been or is assumed to have been observed (interacted) and therefore an effect. All observation is spatial, as is well-known in quantum mechanics. (4) Not only was the problem of the source charge resolved at long last, but also a new and more primary symmetry of energy flow in 4-space was uncovered [[iii]], between the time-domain and 3-space. This new energy flow symmetry is the first principle of free energy and extracting EM energy from the active vacuum.

Fundamentally, when 3-symmetry in EM energy flow is broken, 4-symmetry must then prevail, since conservation of energy requires conservation in 4-space (but not in 3-space per se!) The imposition of EM energy flow conservation in 3-space is an extra requirement. When we inflict the latter additional condition by the way we construct our electrical power systems, then we doom ourselves from ever being able to power systems from the active vacuum alone. Instead, we have assumed the additional burden of putting in all that EM energy for the loads and losses, ourselves. That is why we are raping and destroying the biosphere, the air in our cities, the water in our rivers and lakes and oceans, etc. Our energy engineers and scientists simply will not build electrical power systems that capitalize upon the dipole's broken 3-symmetry in the fierce vacuum energy exchange.

But once we make just a little dipole, nature is most kind. That dipole breaks some of the "additional condition of 3-symmetry" requirement. Hence via the reinterpreted and corrected Whittaker 1903 decomposition of the scalar potential (change in vacuum potential) between the poles of the dipole, we have seen the El Dorado of the free energy researcher's dream: Nature pours in free EM energy to that source dipole from the time-axis, as reactive or "pre-reactive" electrical power. The dipole charges absorb it in the time domain, rotate into 3-space, and re-emit their excitation energy as real 3-space EM energy flow in all directions. The source dipole—if we do not kill it in our circuit designs—will continue to emit that EM energy indefinitely. Further, it emits an enormous, unaccounted "dark energy" flow. For more than a century, we have not paid any attention to catching more of this available dark energy—and efficiently using it to power loads and self-power the generators simultaneously—without using half of what we catch to destroy the source dipole.